Packed Ultra-wideband Mapping Array (PUMA) is a proposed radio telescope operating at 200MHz-1100MHz, optimized for the 21 cm intensity mapping in the post-reionization era but also addressing other science goals amenable to such observations, primarily Fast Radio Bursts (FRBs), pulsar monitoring and transients as a part of multi-messenger observations.

This idea grew up from deliberations of the Cosmic Visions Dark Energy Committee, a panel tasked with investigating possible future directions for Dark Energy program within the Office of Science of the US Department of Energy. A working group has been established that led to the development of a Stage II 21cm experiment that eventually morphed into PUMA.

PUMA Collaboration Workshop, Summer 2020

PUMA Collaboration held an open virtual workshop August 18-20, 2020. Talks can be found here.

Contact PUMA

For inquiries about PUMA or to get onto mailing list, please contact: Anže Slosar (anze AT bnl.gov).

Context

In the next decade, three flagship US-led dark energy projects will be nearing completion: (i) DESI, a highly multiplexed optical spectrograph on the 4m Mayall telescope capable of measuring spectra of 5000 objects simultaneously; (ii) LSST, a 3 gigapixel camera on a new 8m-class telescope in Chile, enabling an extreme wide-field imaging survey to 27th magnitude in six filters; and (iii) WFIRST, a space mission with a significant dark energy component, measuring both spectra and images of galaxies over very small, but very deep fields. These experiments will characterize dark energy at lower redshift with exquisite precision. Together with the continued exploration of the Cosmic Microwave Background (CMB), they will keep the US at the forefront of cosmological observations. Having said that, they will leave a majority of the post-reionization Universe, i.e. within z < 6, uncovered - this range can be fully surveyed via 21cm intensity mapping.

With PUMA, we propose a revolutionary post-DESI, post-LSST program for dark energy, and more, based on intensity mapping of the redshifted 21cm emission line from neutral hydrogen; the field of observation will stretch from our local cosmological neighborhood, at z ~ 0.3, out to z ~ 6, just after reionization. Unlike optical and CMB surveys, which are mature and now planning 3rd and 4th generation experiments, hydrogen intensity mapping is a relatively new technique, but one that offers important complementary science to these planned probes. The PUMA experiment has the unique capability to quadruple the volume of the Universe surveyed by optical programs, providing a percent-level measurement of the cosmic expansion history and growth to z ~ 6. This measurement will significantly improve the precision on standard cosmological parameters, while also opening a window for new physics beyond the concordance LCDM model.

In its full configuration, the total noise will be equivalent to the sampling (Poisson) noise from a spectroscopic galaxy survey of 2.9 billion galaxies (or 600 million galaxies in the more modest, "petite" configuration) on large, linear scales. In addition, multiple cross-correlations with optical surveys and the CMB will dramatically improve the characterization of dark energy and new physics. The rich dataset produced by PUMA will simultaneously be useful in exploring the time-domain physics of fast radio transients and pulsars, potentially in live "multi-messenger" coincidence with other observatories.

PUMA is proposed with six basic science drivers in mind: two relate to fundamental advances in dark energy and modified gravity; two probe the inflationary period; and two touch on astrophysical goals, namely the detection and characterization of FRBs and pulsars. These six agendas can all be fulfilled by the same specialized instrument, as outlined in table below . While these goals inform and primarily determine the design of the instrument, as with any synoptic project, PUMA will open doors to numerous other science goals.

Comparison with existing projects

The design of an instrument to map large swaths of the sky at modest angular resolution, but high sensitivity, is fundamentally different from that of radio telescopes specializing in imaging of individual radio sources. This experiment is therefore not in competition with the ngVLA or SKA. Instead, PUMA is an evolution of a different lineage of experiments, including CHIME, HIRAX, which we refer to as Stage I experiments. Compared to high-resolution imaging arrays, PUMA will be fundamentally different in three aspects:

• The array elements are non-tracking and with considerably simpler mechanical design, but are larger in number
• The array elements are closely-packed together, providing information on the angular scales that matters for the science at hand
• The system provides extremely large instantaneous bandwidth and relies on FFT beam-forming to process the data

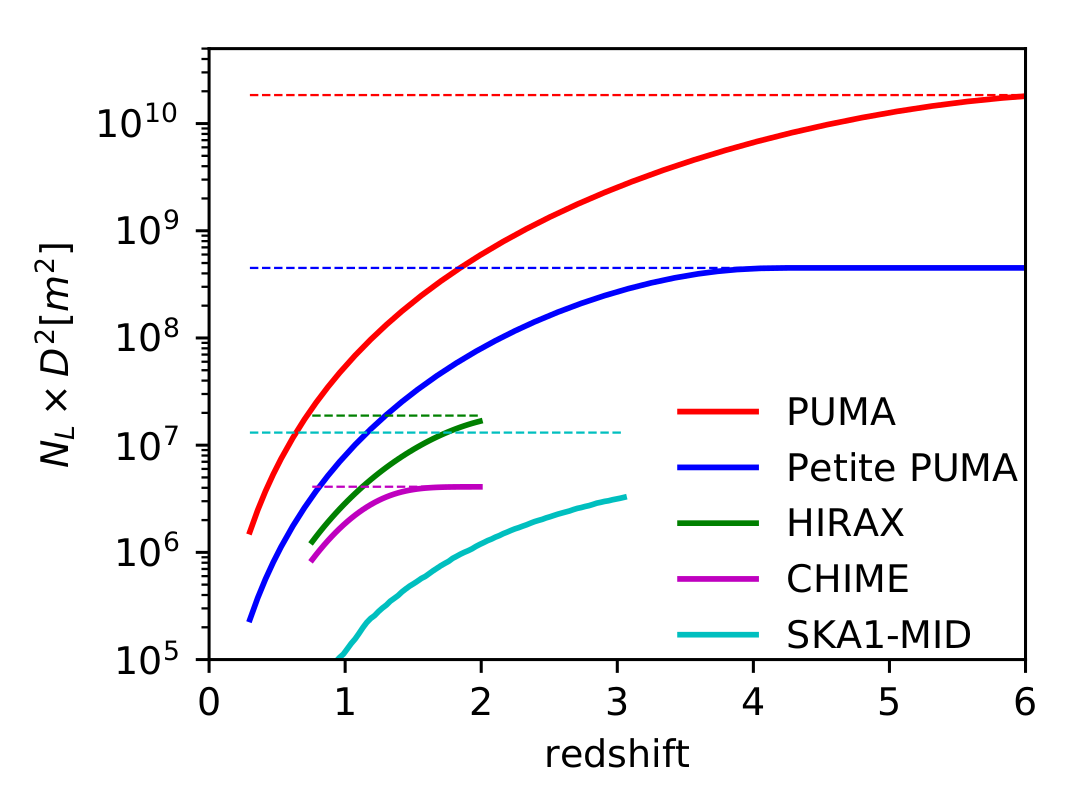
In Figure 1 below , we compare a few relevant experiments in terms of an intensity mapping Figure of Merit (FOM), which is the total number of baselines probing linear scales multiplied by a single element's collecting area.

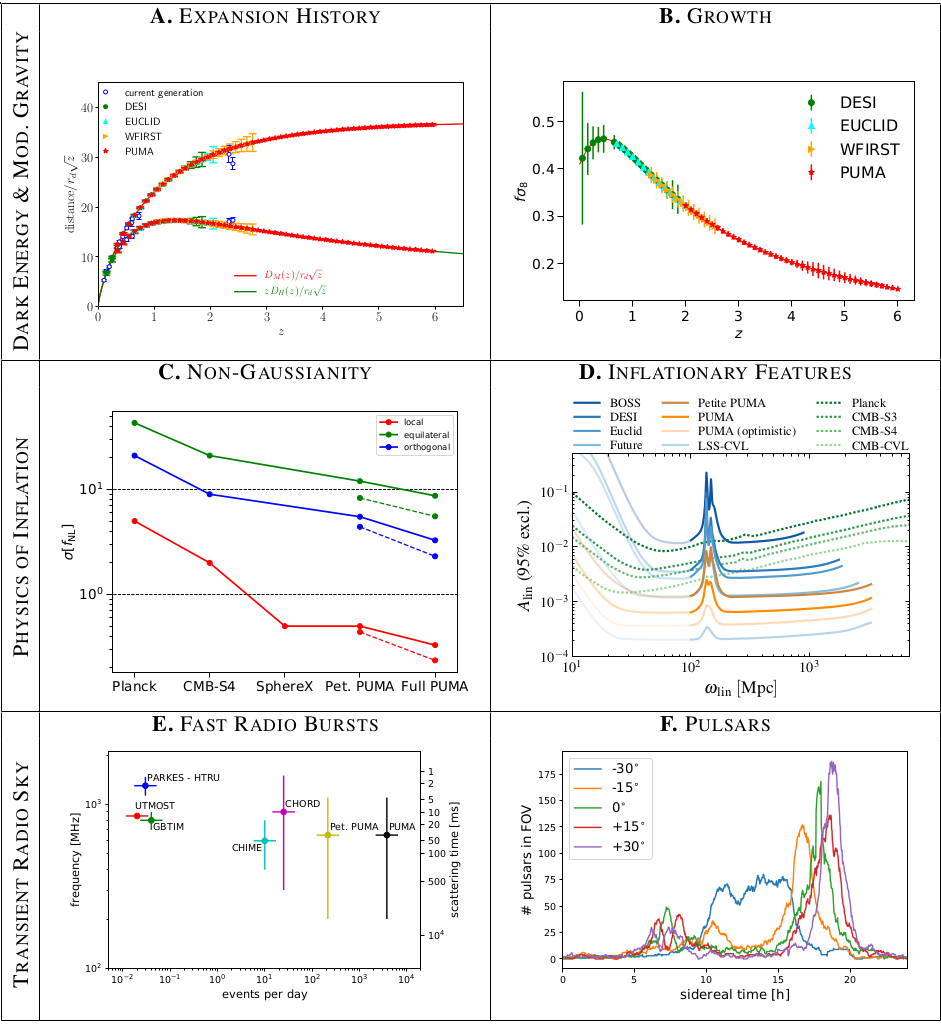
From Science Drivers to Instrument Design

Basic Science Drivers

The PUMA requirements are based on achieving 6 main science drivers from three thematic areas:

Probing the Physics of Dark Energy:

1. Characterize expansion history in the pre-acceleration era. By the time PUMA becomes operational, multiple experiments will have measured the expansion history close to the sample-variance limit out to redshift z ∼ 1.5 and with some precision to z ∼ 3. PUMA will enable nearly sample-variance limited BAO measurements all the way to z ∼ 6 and complete the challenge of characterizing the expansion history across the cosmic ages.
2. Characterize structure growth in the pre-acceleration era. Measuring the growth of structure over the same redshift-range as the expansion history allows fundamental tests of general relativity. If general relativity is correct, then the growth of structure is uniquely determined by the expansion history. A disagreement between the two measurements would be a smoking gun of modified gravity and PUMA is one of the most promising probes to detect it. PUMA will measure growth by relying on the weakly non-linear regime where the degeneracy between bias and growth can be broken by the shape of the power spectrum.

Probing the Physics of Inflation:

3. Constrain or detect the primordial non-Gaussianity. Primordial non-Gaussianity is one of the very few handles that we have on the physics of inflation. Departures from Gaussianity at a detectable level would provide evidence for non-minimal models of inflation which would imply either multiple fields or deviations from slow roll. It would be a monumental discovery, potentially probing physics up to the grand unification scale.
4. Constrain or detect features in the primordial power spectrum. Features in the primordial power spectrum are another, often overlooked, handle on the physics of inflation~\cite{2019arXiv190309883S}. They are generically produced in a wide class of models of inflation and its alternatives. They could provide hints about details in the inflationary potential and, if detected, would have a profound impact on our understanding of inflation.

Probing the Physics of the Transient Radio Sky:

5. Fast Radio Burst Tomography of the Unseen Universe. Fast radio bursts offer a unique probe of the distant Universe if a survey with large numbers of precisely localized sources is available. Faraday rotation provides a precision probe of intergalactic magnetic fields and time-delay microlensing allows for a cosmic census of compact objects (including constraining black holes as dark matter). In addition, dispersion can be used to measure the free electron power spectrum, which breaks a degeneracy for interpretations of kinetic Sunyaev-Zeldovich (kSZ) measurements.
6. Monitor all pulsars discovered by SKA. The SKA1-LOW and SKA1-MID arrays will detect of the order of 3000 pulsars. It is clear that none of the current telescope facilities, including SKA itself, would have enough sky time to follow up the majority of these discoveries. Due to the daily monitoring of a significant subset of these pulsars (depending on the pointing), PUMA will be complementary to SKA, even in the petite array configuration. With its unprecedentedly high timing cadence, PUMA will be able to characterize each of these new pulsar discoveries, and carry out a systematic study of pulsar temporal variabilities, including nulling, glitches, sub-pulse drifting, giant pulse emission, and potential signatures of new fundamental physics.

Science Traceability Matrix

Main Science Goals determine the parameters of the instrument outlined in Key Parameters:

Science Objective	Scientific Measurement Requirement	Measurement objective	Instrument requirements
A. Characterize expansion history in the pre-acceleration era	Measure Baryonic Acoustic Oscillations to volume limited accuracy	Measure 21 cm intensity – over 2 < z < 6 – to k ∼ 0.4hMpc-1 – with SNR per mode ∼ 1 at k ∼ 0.2hMpc-1	Bandwidth must include 200-475MHz Maximum baseline Lmax ≳ 600 m ND > 25km at Lmax = 600m
B. Characterize structure growth in the pre-acceleration era	Measure growth through 21 cm power spectrum on weakly non-linear scales to volume limited accuracy	Measure 21 cm intensity: – over 2 < z < 6 – to k ∼ 1:0hMpc-1 – with SNR per mode ∼ 1 at k ∼ 0.6hMpc-1	Bandwidth must include 200-475MHz Maximum baseline Lmax ≳ 1500 m ND > 200km at Lmax = 1500m
C.Constrain or detect primordial inflationary non-Gaussianity	Measure 21 cm bispectrum to achieve non-Gaussianity parameter sensitivity: – orthogonal: σ [fNLortho] < 10 – equiliateral: σ [fNLequil] < 10	Measure ≳ 109 linear modes with SNR per mode ∼ 1	Same as above plus: bandwidth 200 — 1100MHz (z ∼ 0.3 — 6) assuming fsky ∼ 0.5
D. Constrain or detect features in primordial power spectrum	Constrain features in the matter power spectrum over available scales to – sensitivity σ[Alin] < 10-3	Same as above.	Same as above.
E. Fast Radio Burst Tomography	Volume limited measurement of electron power spectrum, stellar mass census	– 1 million FRBs – covering two frequency octaves – 3” localization precision	Fluence sensitivity threshold ≲ 2.5 fsky Jy ms Provide real-time FRB back-end Provide baseband buffer with triggered readout
F.Monitor pulsars	Monitor all pulsars discovered by SKA	Detect all pulsars in current Field of View brighter than 10μJy	10 σ point source sensitivity >10μJy / transit Provide real-time pulsar back-end

Additional Science

The total science reach of this experiment is considerably wider than the six main goals. In the following, we provide a brief overview of some of the other exciting science capabilities of PUMA:

1. Broadband power spectrum information. In addition to BAO and redshift-space distortion extraction, the exquisite precision with which we measure the linear power spectrum will allow strong constraints to be put on numerous basic parameters, when combined with CMB and other LSS data. Among the parameter constraints forecasted, we would like to emphasize two: i) in combination with CMB-S4, the error on light relics parameter N_eff halves to σ[ΔN_eff] = 0:013; ii) it strongly breaks the m_ν - w degeneracy allowing dark energy parameter of state w to be constrainted with sub percent precision even in cosmologies with free neutrino mass.
2. Weak lensing & Linear Field Reconstruction. The apparent non-Gaussianity of the observed intensity fields will be generated mostly by two mechanisms: weak lensing along the line of sight and non-linear evolution of modes. These effects can be used to reconstruct both the weak lensing potential (analogous to how the CMB measures weak lensing) and the primordial linear density field. New machine-learning inspired methods have the potential to extract almost all information lost to foregrounds exploiting the non-linear cascade of power from large (contaminated) scales to smaller, well-measured scales. The extraction of the primordial linear density field will allow cross-correlation with CMB lensing and galaxy lensing, but also provide a calibration of photometric redshifts in photometric surveys. Moreover, weak-lensing reconstruction will provide more lensing planes allowing for even more cross-correlations, many of which are internal to PUMA and enabled by the extremely large redshift range that is covered.
3. Using PUMA to extract new information from the secondary CMB. Using Sunyaev Zel'dovich (SZ) tomography PUMA will measure a tomographic reconstruction of the remote CMB dipole by appropriate cross-correlations with CMB observations. It can be used to reconstruct long-wavelength radial modes (e.g. those most affected by foregrounds in 21cm intensity mapping) from the statistics of small-scale transverse modes. While SZ tomography can be performed with large photometric redshift surveys such as LSST, doing this with 21 cm intensity mapping offers mapping of more volume at higher signal-to-noise, increasing the reach of the experimnent to fundamental physics. A particular strength of PUMA is the increased redshift range, which helps alleviate astrophysical systematic uncertainties in the forecasts by combining independent information from multiple tomographic bins.
4. Multi-messenger probes. PUMA will have considerable instantaneous field of view (around 1000-2000 square degrees), which will likely cover some of the gravitational wave events by pure coincidence. An immediate trigger from the array of gravitational detectors expected to come online in the coming decade will allow a ring-buffer dump, which would allow reconstruction of any coincident low-frequency counter-part. For transients with knows locations, their fluxes could be measured by dedicating them a number of real-time beamforming beam. PUMA’s pulsar monitoring program will also be able to associate pulsar timing glitches to bursts of gravitational waves due to crustal rearrangements.
5. Direct probe of expansion history. Probing the expansion history of the universe directly, i.e. measuring the redshifts of galaxies in the universe increasing in time would open new avenues for studying the dark energy and gravitational potentials. In optical, this is possible, but fraught with calibration issues, while in radio the clocks are sufficiently stable over a decade can be bought off the shelf. PUMA could make this measurements by either relying on cold absorbers or measure the statistics on overall field. There are significant technical hurdles, but this is a potentially exciting science that deserves further investigation.
6. Time-domain survey for pulsars and magnetars. SKA is set to be the power house in pulsar searching for the southern hemisphere. However, there is still great potential for more discoveries by re-visiting the same sky, as PUMA could observe transient phenomena such as magnetar outbursts or pulses from Rotating Radio Transients (RRATs). PUMA is designed to have a wide field-of-view, a large collecting area and a wide observing bandwidth. As we will be search for FRBs (goal E), we will also have the capability of surveying for other time domain transients.

Antenna Array	Hexagonal close-packed transit array
	Petite	Full	Petite array: Achieve science goals A. & F. and ∼ 30% of B.-E.
array diameter	600m	1500m
fill factor	50%	50%	Full array: Achieve all science goals
number of elements	5,000	32,000
10 σ single transit sens.	8.7μJy	1.3μJy
Array element	Parabolic on-axis with N-S pointing		transit observations, campaign repointing
dish diameter	6m		shortest possible baselines with, D ≫ λmin
construction	on-site fiber glass production, mm surface accuracy		Better beam control than Stage I for systematics
frequency coverage	200 - 1100 MHz
OMT	ultra-wide band, dual-pol
front-end	amplifiers and digitizers integrated with OMT		alternative arrangement to be explored
channelizer	one per 10-100 dishes		helps with corner-turning, alternatives possible
Correlator	FFT correlator with partial N2 correlations		Individual baseline correlation mode for calibration.
FRB capability	real-time FRB search engine
real-time beam-forming	104 concurrent tracking beams		pulsar, transients, multi-messenger

Survey
Area	50% of sky
Observing time	5 years on sky, wall-time 7-10 years
Equivalent source density
at z=2, k=0.2 h Mpc-1	7.4 / 2.0 × 10-3 h3 Mpc-3 (full / petite)
Total equivalent sources
at k=0.2 h Mpc-1	2.9 / 0.6 billion (full / petite)
at k=0.5 h Mpc-1	2.5 / 0.4 billion (full / petite)
FRB rates (expected)
200 - 400 MHz	1200 / 70 per day (full/petite; uncertain)
400 - 700 MHz	1000 / 60 per day (full/petite)
700 - 1100 MHz	1300 / 80 per day (full/petite)
Calibration
complex amplitude	sky sources
primary beam	per antenna calibration using fixed wing drones
clock distribution	100 fs clock distribution for phase stability

For a python module that calculates the noise parameters see Downloads.

Useful links:

• Stage 2 Roadmap
• PUMA Submission to the Astro2020 Decadal Survey
• PUMA Response to RFI for the Astro2020 Decadal Survey
• Costing spreadsheets
• PUMA noise calculator